Quantum Computing Applications - Chemistry
Understanding the properties of chemicals through numerical simulations has been a key enabler for chemical development. But modeling atomic interactions on classical computers quickly exceeds the computational capacity of even the largest supercomputers.
Quantum computers can help. Instead of performing ‘coarse-grained’ approximations on classical computers, scientists can perform much more precise simulations on quantum machines.
A common application for quantum chemistry is searching for the ground state energy of a molecule by finding the minimum eigenvalue of a matrix characterizing it. While this might be done in the future using quantum phase estimation, it can be performed today using much shallower circuits with the Variational Quantum Eigensolver (VQE) algorithm.
Because today’s quantum computers have limited fidelity, it is common to design hybrid quantum-classical algorithms that take advantage of the strengths of each computing paradigm. For instance, the classical computer could perform non-convex optimization and the quantum computer could efficiently calculate the target function. This hybrid approach may prove appealing to solve problems that even Density Functional Theory (DFT) or Hartree-Fock approximations can’t solve.
Here's how it looks with Classiq:
Let’s use Classiq to solve a ground state problem for the molecule H2, starting with our Python SDK. This is done by generating a Hamiltonian, creating a variational quantum circuit to calculate the Hamiltonian’s ground state, and executing said circuit in a hybrid quantum-classical VQE algorithm.
Here we define the problem as an H2 molecule, using the Classiq atom library, specifying their location, charge, and spin. This code block ends in generating the Hamiltonian.
Now, we create an ansatz, or initial parameterized guess for our VQE algorithm, using the Hamiltonian generated. This section of code creates a hardware-efficient quantum circuit to represent the ansatz. The Classiq platform synthesizes quantum circuits in many languages, defaulting to Open QASM 2.0.
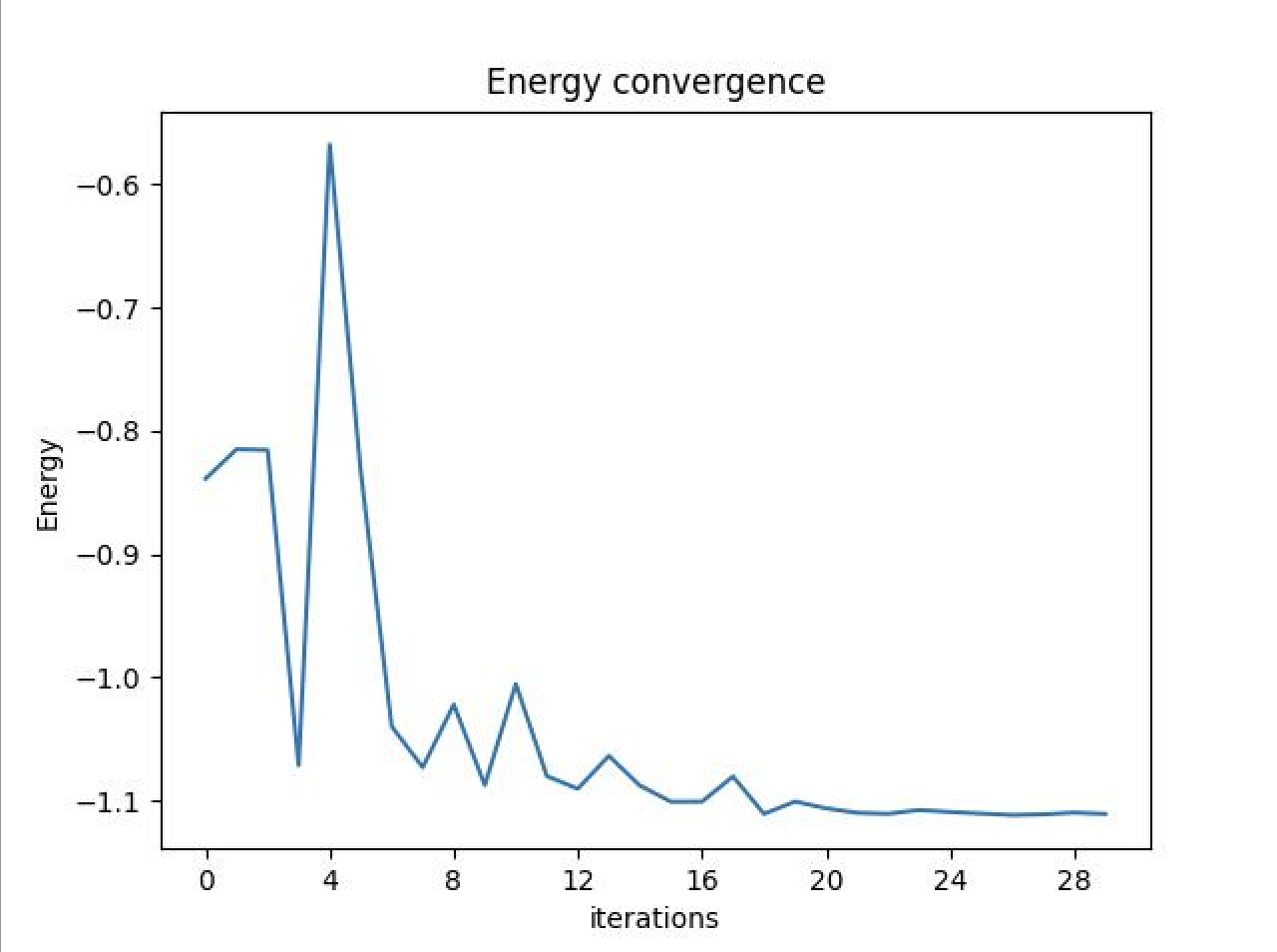
Last, we run the VQE algorithm, iterating 30 times, using the QASM code from the previous section as input and specifying the algorithm is executed by IBMQ's aer simulator.
The ground state energy and optimal parameters are outputted. These parameters correspond to the angles in the ansatz, and our convergence graph shows how the algorithm honed in on the correct solution.

We can do the same process with our Textual Model as well, simply running the following code.
Interested in seeing what the Classiq platform can deliver for your organization? Contact us to schedule a demo

Understanding the properties of chemicals through numerical simulations has been a key enabler for chemical development. But modeling atomic interactions on classical computers quickly exceeds the computational capacity of even the largest supercomputers.
Quantum computers can help. Instead of performing ‘coarse-grained’ approximations on classical computers, scientists can perform much more precise simulations on quantum machines.
A common application for quantum chemistry is searching for the ground state energy of a molecule by finding the minimum eigenvalue of a matrix characterizing it. While this might be done in the future using quantum phase estimation, it can be performed today using much shallower circuits with the Variational Quantum Eigensolver (VQE) algorithm.
Because today’s quantum computers have limited fidelity, it is common to design hybrid quantum-classical algorithms that take advantage of the strengths of each computing paradigm. For instance, the classical computer could perform non-convex optimization and the quantum computer could efficiently calculate the target function. This hybrid approach may prove appealing to solve problems that even Density Functional Theory (DFT) or Hartree-Fock approximations can’t solve.
Here's how it looks with Classiq:
Let’s use Classiq to solve a ground state problem for the molecule H2, starting with our Python SDK. This is done by generating a Hamiltonian, creating a variational quantum circuit to calculate the Hamiltonian’s ground state, and executing said circuit in a hybrid quantum-classical VQE algorithm.
Here we define the problem as an H2 molecule, using the Classiq atom library, specifying their location, charge, and spin. This code block ends in generating the Hamiltonian.
Now, we create an ansatz, or initial parameterized guess for our VQE algorithm, using the Hamiltonian generated. This section of code creates a hardware-efficient quantum circuit to represent the ansatz. The Classiq platform synthesizes quantum circuits in many languages, defaulting to Open QASM 2.0.
Last, we run the VQE algorithm, iterating 30 times, using the QASM code from the previous section as input and specifying the algorithm is executed by IBMQ's aer simulator.
The ground state energy and optimal parameters are outputted. These parameters correspond to the angles in the ansatz, and our convergence graph shows how the algorithm honed in on the correct solution.


We can do the same process with our Textual Model as well, simply running the following code.
Interested in seeing what the Classiq platform can deliver for your organization? Contact us to schedule a demo
About "The Qubit Guy's Podcast"
Hosted by The Qubit Guy (Yuval Boger, our Chief Marketing Officer), the podcast hosts thought leaders in quantum computing to discuss business and technical questions that impact the quantum computing ecosystem. Our guests provide interesting insights about quantum computer software and algorithm, quantum computer hardware, key applications for quantum computing, market studies of the quantum industry and more.
If you would like to suggest a guest for the podcast, please contact us.



.svg)











